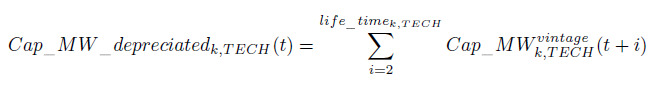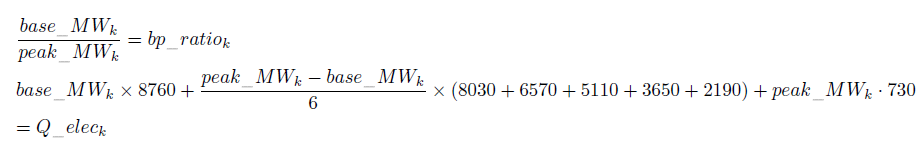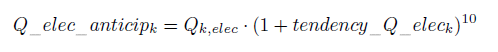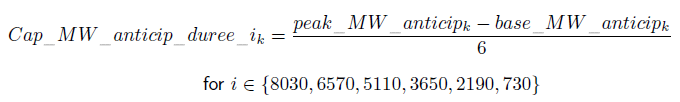Electricity - IMACLIM
| Corresponding documentation | |
|---|---|
| Previous versions | |
| Model information | |
| Model link | |
| Institution | Centre international de recherche sur l'environnement et le développement (CIRED), France, http://www.centre-cired.fr., Societe de Mathematiques Appliquees et de Sciences Humaines (SMASH), France, http://www.smash.fr. |
| Solution concept | General equilibrium (closed economy) |
| Solution method | SimulationImaclim-R is implemented in Scilab, and uses the fonction fsolve from a shared C++ library to solve the static equilibrium system of non-linear equations. |
| Anticipation | Recursive dynamics: each year the equilibrium is solved (system of non-linear equations), in between two years parameters to the equilibrium evolve according to specified functions. |
Generating electricity: taking account of load curve constraints
The electricity production sector is particularly influenced by climate policies since it is the sector with the highest greenhouse gas emissions. In 2004 it was responsible for 20% of worldwide emissions of the six gases covered by the Kyoto Protocol. Emissions grew by 53% between 1990 and 2004 to reach 10.7 Gt of CO2 in 2004. These emissions are caused by the combustion of fossil resources, namely coal, oil and gas, in power plants.
The production and technological choices taken in the electricity sector arise from the difficulty associated with storage of the sector main output: electricity. In an electricity distribution network it is necessary to ensure a constant balance between the power available and the power demanded by the sum of final end uses (the load). Production must therefore adapt to major fluctuations in daily and seasonal network demand. Facing the uncertainty of future real demand, possible breakdowns and the intermittence of certain production means (renewables), a centralized producer must choose between a level of risk of electricity supply shortages and the construction of spare or auxilary capacity. When the electricity market is liberalized, this control of the evolution of capacities becomes more difficult unless one of the producers has sufficient scale to assure adjustment of the total capacities according to the needs of the economy (e.g. EDF in France). Correspondingly, the profitability of production technologies - or put another way, the total production cost per kWh - depends on the annual operating time, fixed and variable costs for each respective production technology as well as on operational technical constraints. Therefore, both long term investment choices and choices concerning putting existing capacities into operation depend on the network load curve, a curve which indicates the evolution of power demanded by the network over time.
The detail of a top-down / bottom-up model hybridization are particularly palpable here: without the physical and temporal constraints of the network load curve, the choice of electricity production technologies would be simply oriented towards the cheapest technology available although eventually taking other constraints into account (social acceptability, investment risk, size of production units, market structure, etc.). However, due to the variation in the load curve, the representation of investment choices and the decision to dispatch existing capacities is complex. This complexity can be decomposed as consisting of the following components:
- A detailed representation of the large types of technologies that can be distinguished by their cost characteristics and their own physical or socio-economic constraints (basic or cutting edge technologies, limited potential, social and environmental acceptability, etc.);
- An explicit representation of the load curve and its evolution over time;
- An investment optimization procedure dependant on the projected future load curve and long term price and demand expectations;
- A decision mechanism for choosing when to dispatc hexisting production capacities according to the load curve and current primary energy prices.
We describe each of these elements in detail in the following four sub-sections.
Explicit production technologies described in terms of capital generation
The description of the power generation mix is based on a discrete set of 13 technologies. Each of the 13 technologies is characterized by a set of techno-economic parameters that make it possible to calculate their average discounted production cost per kilowatt hour produced. These parameters include: capital costs ($/kW installed), energy efficiency (in %, for the technologies that use fossil fuels), operation and maintenance costs, fixed or variable costs (in $/kW and in $/kWh respectively) and a discount rate incorporating both the opportunity cost of capital and a unique risk factor for each technology. This risk factor can cover both an objective assessment of the risk of outage as well as an assessment of social risk, for example for the cases of nuclear power or CCS (Carbon Capture and Sequestration). The techno-economic parameters associated with each technology are calibrated either from sectoral technological models (for example the POLES model) or using information from literature (Grubler et al, 2002grubler2010technological; Rao et al, 2006rao2006importance; Sims et al, 2007sims2007energy).
<xr id="tab:discount_cost"/> gives the calibration values for the United States of the techco-economic parameters characterizing the 13 technologies described in this version of the model. The last four rows of the table contain the calculation results for each technology at the year of calibration and the different components of the discounted average production cost: investment cost, operation and maintenance cost, fuel cost, for an annual usage duration of 8760 hours (One year).
<figtable id="tab:discount_cost">
| Natural gas | Natural gas | Natural gas | Coal | Coal | Coal | Coal | Coal | Renewables | Renewables | Renewables | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | Notation in equations | Unit | Oil | Simple Cycle | Combined Cycle | Combined Cycle with CCS | Thermal | Super critical | Super critical with CCS | Gasification and combined cycle | Gasification and combined cycle with CCS | Nuclear | Hydro | Onshore Wind | Offshore Wind |
| Operational at the calibration year | yes | yes | yes | no | yes | no | no | no | no | yes | yes | yes | no | ||
| Investment Cost | CINV_KW | $2001/kw | 1000 | 400 | 500 | 1120 | 1050 | 1600 | 2700 | 1500 | 2400 | 2600 | 2000 | 1400 | 1800 |
| Fixed OPEX(Operation expenditure) | OM_Cost_fixed | $2001/kw | 15 | 26 | 10 | 50 | 53 | 35 | 60 | 37 | 70 | 58 | 20 | 50 | 50 |
| Life Time | life_time | Years | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 45 | 20 | 20 |
| Discount rate | disc | % | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| Variable OPEX | OM_Cost_var | $2001/kWh | 0.0017 | 0.0014 | 0.0014 | 0.0022 | 0.0024 | 0.0028 | 0.0034 | 0.0024 | 0.0029 | 0.0012 | |||
| Cost of fuel | $2001/Toe | 237 | 160 | 160 | 160 | 71 | 71 | 71 | 71 | 71 | |||||
| Energy Efficiency | rho_elec | % | 36 | 35 | 53 | 47 | 35 | 45 | 35 | 42 | 36 | ||||
| Availability rate | % | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 20 | 24 | |
| Average discounted investment cost | $2001/MWh | 12.1 | 4.8 | 6.1 | 13.6 | 12.7 | 19.4 | 32.7 | 18.2 | 29.1 | 31.5 | 23.1 | 93.9 | 100.6 | |
| Average discounted fuel cost | $2001/MWh | 56.6 | 39.3 | 26.0 | 29.3 | 17.4 | 13.6 | 17.4 | 14.5 | 17.0 | 5.0 | 0.0 | 0.0 | 0.0 | |
| Average discounted operation and maintenance cost | $2001/MWh | 5.3 | 3.0 | 1.5 | 6.1 | 6.1 | 4.0 | 14.1 | 4.2 | 17.0 | 7.8 | 2.3 | 28.5 | 23.8 | |
| Average discounted production cost | $2001/MWH | 74.0 | 47.1 | 33.5 | 48.9 | 36.2 | 36.9 | 64.2 | 36.9 | 63.0 | 44.3 | 25.4 | 122.4 | 124.3 |
For the technologies listed in <xr id="tab:discount_cost"/> which are classed as being mature (See Row 3: Operational at the calibration year) the data given corresponds to the model reference year (2001). Data in the table for technologies that are not considered to be mature yet, corresponds to various years which are dependant on the scenario under consideredation. The data are not, however, averages for each region in the calibration/reference year, since the installed capacity of production plants also include less efficient older production units. Likewise, at future dates in the scenarios modeled, the average characteristics of the installed production capacity will be the weighted average of the technical characteristics of the different generations of power plants still in operation. The inertia of equipment and the embodied character of technologies are represented through a follow up of capital through the generations along with that of their technological characteristics. Hence, each unit of a given technology's production capacity constructed at time t is active until t+life_timek,TECH, where life_timek,TECH is the expected technology lifetime in region k for each technology, TECH. The overall installed production capacity park at time t is decomposed according to the duration of the year in which the various production units are dispatched. For each technoloy TECH and each region k, the electricity production capacity (measured in MW) is obtained by summing up the generations of capital in activity:
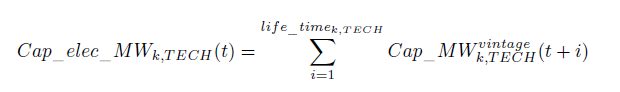
Every year (t+1), the production capacities that reach the end of their lifetimes are eliminated (lifetime varies according to the type of technology installed). One thus obtains a depreciated installed production capacity, Cap_MW_depreciatedk,TECH. At each time period this is combined with the new investments to obtain the total installed production capactity:
The capacity of the new generation of capital ![]() and its technological characteristics is determined by electricity producers investment choices, represented as described in the following sections.
and its technological characteristics is determined by electricity producers investment choices, represented as described in the following sections.
Physical and temporal constraint of the load curve
The production load curve represents the time dependence of the power generated by a system. It meets the demand fluctuation at the scale of a day or a season.
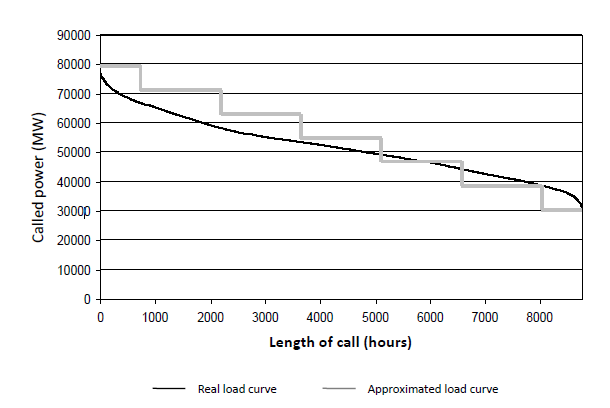
In order to model investments, it is common to aggregate the daily load curves over the 365 days of the year into a single curve called a monotonous load curve divided into 8760 hourly segments. This monotonous load curve decreases depending on the load duration averaged over the year (i.e. not in the chronological order of power dispatch). The maximum load over the transmission network (peakload) is given by the maximum of the curve at its intersection with the Y-axis. The minimal level of power that is supplied throughout the year is the value of this monotonous load curve over the 8760 hours (baseload).
The shape of the monotonic power is unique to each region because it is directly linked to the temporal variability of the electricity demand. This variability depends on the seasonal climate variations of the region as well as on the nature of the electricity demand e.g. over time household demand is much more variable than that of the industrial sector. For numeric simplicity, the monotonous regional load curves have been schematized as segmented linear functions (See figure below) according to the following specifications:
- The possible annual loads (measured in hours) are divided into seven intervals with the following boundaries: (0, 730, 2190, 3650, 5110, 6570, 8030, 8760);
- The maximum load lasts for a duration of 730 hours (peakload);
- The minimum load lasts for a duration of 8760 hours (baseload);
- The load level for the other periods of time is calculated by dividing the interval between baseload and peakload into six equal segments i.e. 760 hours of baseload, 760 hours of peak load and five segments in between of 1460 hours each.
Using this simplified scheme, the monotonous load curve of each region can be thus completely characterized by two parameters: peakload and baseload.
The monotonous load curve also links the production capacities (expressed in megawatts) and the quantity of energy produced annually (measured in megawatt hours or other energy units) by dispatching existing capacities in a flexible manner according to demand on the network. The annual electricity produced is obtained simply by calculating the total of the monotonous load curve for the interval [0 to 8760] and is equivalent to the surface beneath the curve presented in the figure below.
FIGURE CAPTION: Example of monotonous load curve approximation method.
The calculation of produced energy based on the installed capacity is carried out at every step of the simulation to recalibrate the technical coefficients of the electricity sector. These depend on the dispatch choices of the installed capacity according to the variable costs of each type. The reverse calculation of installed capacities from energy produced, is necessary during investment programming because it is important to know how the monotonous load curve corresponds to the anticipated annual energy demand.
To calibrate and reconfigure the monotonous load curve at each time period, we assume that the ratio of peakload to baseload, (written bp_ratiok) remains constant and equal to a value supplied by the POLES model.In principle, this ratio could vary in an exogenous or endogenous manner to integrate, for example, its modification under the effect of policies of demand management. However, in the current version of the model it is kept constant. Using our method of approximating the monotonous load curve into linear segments, the calculation of the monotonous load curve associated to a quantity Q_eleck of electricity produced in region k, is obtained by solving the equation system, formed by the ratio constancy equation and the constraint equation on the quantity of energy produced:
where base_MWk and peak_MWk are the power levels required during the base or peak periods respectively.
Optimal planning of investments in imperfect foresight
With the compact representation of electricity production technologies and the load curve that has been presented above, we posess the necessary technical details to model investment choices in the electricity sector for each date t, choices which will progressively modify the size and technical composition of the installed capacity. It is more explicitly a question of representing an optimal planning procedure given imperfect foresight, a procedure which determines the make-up of the installed capactity in the current time period and and the investment necessary to meet projected future electricity demand while minimizing the average total cost of production.
The decision-making procedure is decomposed into five successive steps:
- Projecting future demand and future fuel prices;
- Choosing wind turbine electricity production capacities;
- Choosing hydroelectric production capacities;
- Projecting the optimal conventional (non-renewable) production capacity (the optimal installed capacity) to meet residential demand;
- Deciding on the annual investment increase necessary to move the existing production capacity towards the optimal capacity that has just been calculated (see previous bullet point).
Separating the treatment of wind and hydroelectric energy is justified by the specificities of these energy carriers. A more detailed explanation of these specificities is given below.
Projecting demand and anticipating fuel prices
The optimal installed capacity and level of annual investments are determined using adaptive anticipation of electricity demand growth and future fossil fuels prices over the coming ten years.
The regional projections of electricity production for the period t+10, written Q_elec_anticipk are calculated on the basis of the current growth rate of electricity production, tendency_Q_eleck which is taken to be stable for the next ten years, and the current electricity production, Qk,elec (in megawatt hours).
Anticipated electricity production from conventional (non-renewable) energy carriers is associated with an anticipated monotonous load curve which is determined using the results from the resolution of the equation system given above. The installed production capacity in the t+10 period should also supply a baseload base_MW_anticipk, and a peakload peak_MW_anticipk. Production capacities Cap_MW_anticip_duree_ikare defined by the equation below and issued for the different segments of the load curve (8030, 6570, 5110, 3650, 2190, 730):
As far as fuel prices are concerned, we confine ourselves to a "myopic" anticipation hypothesis: current prices are taken as anticipated future prices. We thus suppose that facing the uncertainty of short-term fluctuations in fossil resources prices, electricity producers take current prices as the best available information. In addition the agents are taken to be myopic about the carbon tax profile fixed by the regulator in the stabilization scenarios. The anticipated values of taxed prices for the three fossil fuels, coal, oil and gas, are written respectively p_coal_anticip_taxedk, p_oil_anticip_taxedk and p_gas_anticip_taxedk. For electricity production technologies which use CCS, a specific attenuation coefficient is applied to the tax so that only the diminished CO2 emissions are taken into account. In future versions of the model, we plan to introduce more sophisticated modes of anticipation, notably the possibility of representing a range of price anticipations and an optimization approach under uncertainty.
Determining upstream investments in non-hydroelectric renewable production capacities
Non-hydroelectric renewable energies are treated separately because of (i) the intermittent character of their electricity production, (ii) the possibilities of decentralised production of renewable electricity, for example in buildings, which by satisfying part of the demand reduce the total demand on the network. In the current version of the model, these two characteristics are taken into account in an aggregated manner in the form of three hypotheses:
- The only renewable energy explicitly represented in the investment choices of the supply mix is wind turbine energy, either on- or off-shore. It is assumed that solar energy is used only when integrated in buildings, making it possible for them to satisfy part of the residential needs through this decentralized production and also to reduce demand to below the 50 kWh/m2/yr threshold we categorise as a VLE building.
- In fact, the dimensioning of wind farms is made through the allocation of production from wind in the total energy production, share_ENR_eleck. This share is assumed to depend on the ratio between the total production cost of wind energy (per kWh) and the total minimal anticipated baseload electricity production with conventional technologies. The value of this share varies according to the region under consideration taking into account (i) the physical limits of the penetration of of intermittent renewable electricity on the distribution network (although in certain cases, the distribution of wind turbines/farms across the region can guarantee a given power almost all year long) and (ii) constraints linked to saturation of the regional renewable production potentials. In the default setting of the model, it is assumed that ithis value cannot exceed 40 % in any region. The quantity of wind turbine energy in the optimal production capacity at t+10 is therefore given by the equation:
- Progressive planning of investments to assure the necessary production capacities to furnish this wind turbine energy - written Cap_elec_MW_anticipk,TECH_ENR- again requires a split between onshore and offshore wind turbines, a split which depends on the relative profitability of the two categories of technology. In addition, in order to determine the production capacity that must be installed to meet a certain energy production in each of these two categories, the average availability factor of each technology is be taken into account.
Investment in hydroelectricity
The quantity of power remaining to be supplied, in addition to that provided by wind turbines (described in previous section), is written Q_elec_CONV_anticipkand is obtained by subtracting the energy that will be supplied by the wind turbines under construction from the total anticipated demand. The available hydroelectric capacities - rather than other conventional forms of energy - are dispatched first from the conventional production capacity that will be needed to supply Q_elec_CONV_anticipk.
Hydroelectricity is treated in a specific manner because investments in this technology are both dependent on its relative profitability and on the available geographical sites. In this module we make no distinction between run-of-the-river and conventional (dammed) hydro power plants and hydroelectric production capacities are dispatched with reference to all other conventional technologies to meet the baseload or higher levels.
In each region covered by the model, information calibrated on the MARKAL model (Labriet et al., 2004)labriet2004advanced supplies the potential volume of hydroelectric production that are technically exploitable (expressed in gigawatts). In the same manner as for wind energy, the electricity sector anticipates the share of hydroelectricity that will be needed during the period t+10 by comparing the complete production cost per kWh of new hydro capacity with the total minimum anticipated electricity production cost in the set of other conventional technologies during the baseload period. By applying this share to the regional potential of hydroelectric production, the model assumes a prioritisation of the dispatch of hydroelectric production capacity, Cap_elec_MW_anticipk,Hydro, for the long production periods (baseload and the dispatch segment just above it).
In order to determine the remaining conventional production capacities to satisfy the anticipated monotonous power load curve constraint, the optimization calculation of the conventional installed capacity without hydroelectricity will be made on the monotonous load curve truncated at the bottom at a power equaling the anticipated hydroelectric production capacities.
Conventional installed production capacity
The 'Residual' monotonous power load curve is that remaining once the wind and hydroelectric capacities have been deducted. It determines for all 7 segments of the annual utilization period, a portion of the conventional production capacity that should be available at date, t+10. In the projected least cost installed production capacity certain capacities will be constructed to be used in the base load period (that is to say, 8760 hours per year) while others will be constructed to be used 8030 or less hours per year up to the peak capacities which will be used only 730 hours per year.
Planning the conventional installed production capacity at minimal cost for the period, t+10, means determining, for each discrete segment of annual utilization, the cheapest production technology. Assessing the competitiveness of a technology to satisfy a fixed annual utilization period is done by calculating the discounted total production cost of a kilowatt hour for this availability factor. This total cost corresponds to the total discounted cost over the equipment lifetime of a kilowatt of installed capacity that includes:
- The capital cost or construction cost
- The fixed total discounted operation and maintenance costs per kWh installed
- The variable total discounted operation and maintenance costs per kWh produced
- The total discounted fuel costs, calculated using the final price scenarios of the anticipated fossil energies.
The total discounted cost for the technology lifetime in each segment of the utilization period serves as the basis for calculating the fixed annuity equivalent to paying this discounted total cost. The total discounted production cost of a kilowatt-hour for this utilization period is then obtained by dividing this annuity by the kilowatt-hour produced.
Calculating the total discounted production cost of a kWh for each conventional technology makes it possible to determine the technologies that are most profitable for each possible annual availability factor. The penetration of these technologies will thus be favoured in the new capacity installed however without allowing them to capture the entire market. Market heterogeneities and uncertainties linked to the discounted production costs mean that for the purpose of modelling diversifying the portfolio of technologies and their coexistence within the same installed capacity of competitive technologies, is justified (Clarke and Edmonds, 1993)clarke1993modelling.
Specifically, the partitioning of the different technologies among the anticipated production capacities dedicated to an annual use of fixed length is carried out according to a logit function. For each utilization period, this logit function is calibrated to the reference year to reproduce the observed market shares of the period according to the anticipated production costs calculated in the model. These anticipated costs incorporate an additional cost called the intangible cost, of which the value makes it possible to calibrate the market shares of the different technologies in the reference year to the observed values of the electricity sector in the regions of the model at the same date.
The capacities of the optimal conventional installed capacity at t+10, (Cap_elec_MW_anticipk,TECH) are obtained by summing up the desired production capacities of the 7 segments of the load period.
Calculating the current investment: minimizing the distance between the optimal production capacity and the installed capacity
The procedure described in the preceding sub-section allows us to define at each date, t, the optimal anticipated production capacity for the period t+10. Investment decisions at date t then aim at reorienting the existing production capacity towards the optimal anticipated production capacity by the end of the decade, under the constraints of available capital.
To achieve the anticipated optimal capacity at t+10, one needs only to make capacities evolve in 10 equal time steps. For example, between t and t+1, the evolution in capacities will be given by the equation below. However, this evolution can face financial constraints on the one hand and the need to depreciate certain capacities before the end of their life time on the other.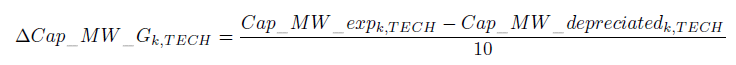
In the present version of the model, it is not possible to either remove certain production capacities before the end of their life-time or modify the technologies embodied in the installed capacities, i.e. there is no early decommissioning or retrofitting. We thus treat the inertia of the equipment and technologies as if they are utilized for their full life-time. This hypothesis makes it necessary to rewrite the above equation under the double constraint of:
- Disposing of no disinvestments for certain technologies;
- Not obtaining a total size of new investments (in megawatts) that would lead to an over-dimensioned installed electricity capacity for the period t+1 with reference to anticipated electricity production.
The composition of the actual investment made, written Inv_MWk,TECH, is obtained by solving a program for minimizing the difference between the investment made and the net desired investment under the constraint of the quantity of capital actually allocated to the electricity sector, Inv_elec_valk.
This investment generates a new generation of capital that marginally modifies the composition of the installed electricity production capacity for the next static equilibrium:
On the basis of this new installed generation capacity, the new technical parameters characterizing thetechnologies embodied in the electricity sector capacities remain to be calculated so as to solve the next static equilibrium.
Calculating average production cost from the installed generation capacity
Once investments have been made according to imperfect foresight of future prices and demand, the actual division of production across the existing production capacities depends on the real load curve. For the model to be completely coherent, the day-to-day operating choices for the different capacities must be integrated into a static equilibrium since they are no longer a question of long term investment choice but rather of short term considerations which depend on instantaneous energy market conditions. Nevertheless, it was judged that integrating these choices into the static equilibrium was too complex, and so they were left in the preceding dynamic module. In this approach, an approximation is made by calculating the technical coefficients of the electricity sector on the basis of projected fossil fuel prices at t+1 instead of calculating them on the basis of actual variables.
In every region of the model, electricity producers make an estimate of the electricity production that needs to be constructed for the following period. The average installed capacity of wind energy estimated in its planning meets some of this production. This wind energy produced is then deducted from the total anticipated demand.
The electricity sector then anticipates that the residual demand is split up according to an anticipated monotonous load curve calculated by following the same procedure as before but at t+1 instead of t+10. The electricity sector next tries to minimize production cost variables so as to meet the demand not satisfied by the electricity from wind power by taking account of the anticipated monotonous load curve. The control variable is the anticipated availability factor for each installed unit of production capacity. Depending on the current prices of fossil energies calculated in the preceding static equilibrium, the technologies of conventional production are classified according to increasing variable production cost. The projected monotonous load curve determines the seven load segments associated to the seven discrete utilization periods. The available production capacities are used by increasing variable costs to supply the power demanded per segment of decreasing utilization periods. In practice this approach shows that the technology with the lowest variable production cost will be used for the longest utilization periods (e.g baseload) until:
- Either the power called for exceeds the available production capacity for this technology and the next cheapest installed production capacity is exploited to obtain the additional power,
- Or the available production capacities of this technology exceed the power demanded for this load duration and the remaining available production capacities will be used to answer demand associated with the load duration that is immediately inferior.
The figure below gives a stacked example of the technologies by order of merit according to their lengths of use. 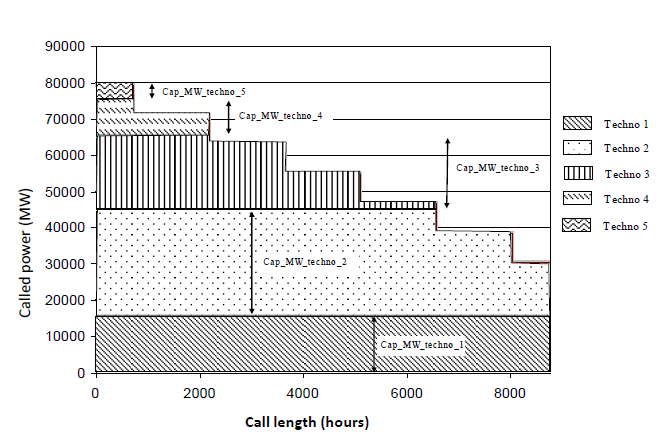
FIGURE CAPTION: Example of the calculation of the annual utilization periods for the five different technologies classified according to increasing variable production cost (technology n°1 has the lowest variable production cost and n°5 the highest) and of which the available production capacities, written Cap_MW_techno_i for i belonging to the discrete set (1; 2; 3; 4; 5).
This production cost minimization program makes it possible to associate an average annual utilization period (in hours) in each region k to each stock of installed production capacity using technology, TECH. The product of these two terms makes it possible to determine the quantity of electricity actually produced by the technology under consideration.
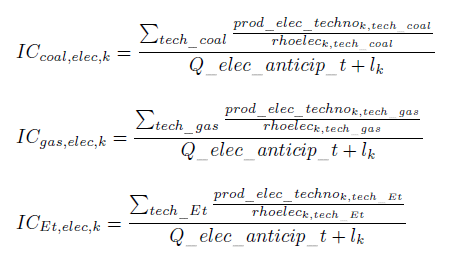
For conventional technologies using fossil fuels, the fuel consumption associated to the electricity produced is calculated directly from the average energy efficiency of electricity generation of the installed capacity of the technology.
The technical unitary coefficients of production which characterize the electricity sector (quantities of different fuels required to produce a unit of electricity) are determined for coal, gas and liquid fuels by the three equations below: