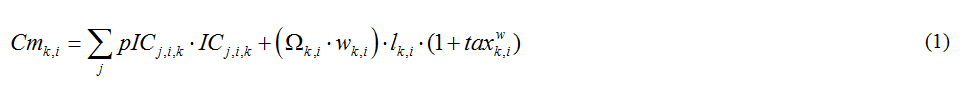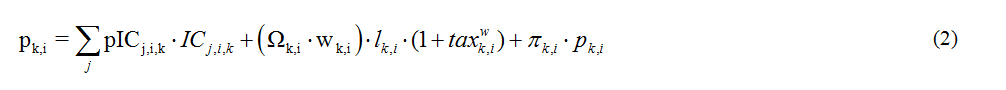Production system and representation of economic sectors - IMACLIM
| Corresponding documentation | |
|---|---|
| Previous versions | |
| Model information | |
| Model link | |
| Institution | Centre international de recherche sur l'environnement et le développement (CIRED), France, http://www.centre-cired.fr., Societe de Mathematiques Appliquees et de Sciences Humaines (SMASH), France, http://www.smash.fr. |
| Solution concept | General equilibrium (closed economy) |
| Solution method | SimulationImaclim-R is implemented in Scilab, and uses the fonction fsolve from a shared C++ library to solve the static equilibrium system of non-linear equations. |
| Anticipation | Recursive dynamics: each year the equilibrium is solved (system of non-linear equations), in between two years parameters to the equilibrium evolve according to specified functions. |
Productive sectors
A start point for IMACLIM is the recognition that it is almost impossible to find mathematical functions that can handle large departures from a reference equilibrium over a time period of one century and are flexible enough to encompass different scenarios of structural change resulting from the interplay between consumption styles, technologies and localization patterns (Hourcade, 1993)hourcade1993modelling.
Beyond the classical production function, or reconciling bottom-up and top-down approaches
In IMACLIM-R, there is no production function, such as a constant elasticity of substitution function, to represent evolutions in production techniques (substitutions between production factors). Instead, evolutions in production techniques are represented in a recursive structure by an exchange of information between static and dynamic modules described as follows:
- An annual static equilibrium module, in which the production function mimics the Leontief specification, with fixed equipment stocks and fixed intensity of labor, energy and other intermediary inputs, but with a flexible utilization rate. Solving this equilibrium at time, t, provides a snapshot of the economy at this date showing a set of information about relative prices, levels of output, physical flows and profitability rates for each sector and allocation of investments among sectors.
- Dynamic modules, including demography, capital dynamics and sector-specific reduced forms of technology-rich models, which take into account the economic values of the previous static equilibrium, assess the reaction of technical systems and send back this information to the static module in the form of new input-output coefficients for calculating the equilibrium at time, 't' + 1. Each year, technical choices are flexible but they modify only at the margin the input-output coefficients and labor productivity embodied in the existing equipment that result from past technical choices. This general putty-clay assumption is critical to represent the inertia in technical systems and the role of volatility in economic signals.
This modelling approach allows for abandoning standard aggregate production functions, which have intrinsic limitations in cases of large departures from the reference equilibrium (Frondel et al., 2002)frondel2002capital and sea changes of production frontiers over several decades.
As we move away from using a traditional production function, it becomes possible to highlight the influence of factors other than price on decisions affecting the allocation of resources. The use of this modeling approach requires however a comprehensive description of the temporally evolving technical characteristics of each sector.
At each point in time, producers are assumed to operate under constraint of a fixed production capacity Capk,i, defined as the maximum level of physical output achievable with their installed equipment.
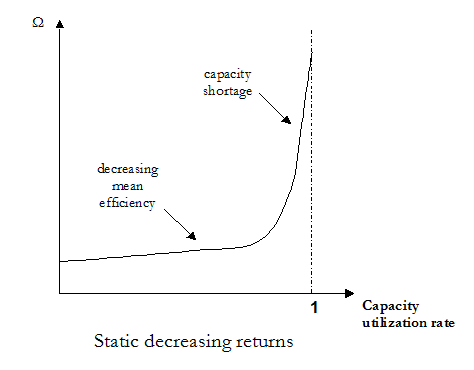
However, the model allows short-run adjustments to market conditions through the modification of the utilization rate Qk,i/Capk,i. This represents a different approach from standard production specifications, since in Imaclim the 'capital' factor is not always fully utilized. Supply cost curves in Imaclim-R thus show static decreasing returns: production costs increase when the utilization rate of equipment approaches 1 (100 %) (See <xr id="fig:imaclim_4"/>). In principle, these decreasing returns affect all intermediary inputs and labor. However, for the sake of simplicity and because of the order of magnitude of the correlation between utilization rates and prices (Corrado and Mattey, 1997)corrado1997capacity, we assume that the primary cause of higher production costs is higher labor costs due to overtime operations with lower productivity, costly night work and increased maintenance works. We thus set (i) fixed input-output coefficients representing that, with the current set of embodied techniques, producing one unit of good i in region k requires the fixed physical amount ICj,i,k of intermediate goods j and lk,iof labor; (ii) a decreasing return parameter Ωk,i= Ω(Qk,i/Capk,i) on wages only, at the sector level. The treatment of the cost of crude oil production is an exception. The increasing factor weighs on the mark-up rate, to convey the fact that oligopolistic producers can take advantage of capacity shortages by increasing their differential rent.
This solution actually comes back to earlier works on the existence of short-run flexibility of production systems at the sectoral level with putty-clay technologies (Marshall, 1890)marshallpoe, (Johansen, 1959)johansen1959substitution demonstrating that this flexibility comes less from input substitution than from variations in differentiated capacity utilization rates.
<figure id="fig:imaclim_4">
</figure>
Equations
We derive an expression of mean production costs Cmk,i, that depends on the prices of intermediate goods pICj,i,k, input-ouput coefficients ICj,i,k and lk,i, wages wk,i, and production levels through the decreasing return factor Ωk,i applied to labor costs (including payroll taxes).
Market prices and associated profits depend on assumptions regarding the degree of market competition in each sector (e.g. perfect competition or monopoly). Unless otherwise stated, perfect competition is assumed in every production sector, with the market price equal to the marginal production cost.
Producer prices are equal to the sum of mean production costs and mean profits. In the current version of the model, all sectors apply a constant sector-specific mark-up rate pk,i so that the producer price is given by equation (2). This constant mark-up corresponds to a standard profit-maximization for producers whose mean production costs follow equation (1) and who are price-takers, provided that the decreasing return factor can be approximated by an exponential function of utilization rate.
This equation is an inverse supply curve: it shows how a representative producer decides their level of output Qk,i (which is included in the Ωk,ifactor) as a function of all prices and real wages.
From equation (2) we derive wages and profits in each sector:
The cost function shows fixed technical coefficients and therefore does not allow for substitution between production factors when relative prices change within the new static equilibrium. Only the level of output Qk,i can be adjusted according to these price changes.