Snapshot of - IFs
Archive of IFs, version: 7.36
Reference card - IFs
The reference card is a clearly defined description of model features. The numerous options have been organized into a limited amount of default and model specific (non default) options. In addition some features are described by a short clarifying text.
Legend:
- not implemented
- implemented
- implemented (not default option)
About
Name and version
IFs International Futures 7.36
Model link
Institution
Frederick S. Pardee Center for International Futures, University of Denver (Pardee Center), Colorado, USA, https://pardee.du.edu/.
Documentation
IFs documentation consists of a referencecard and detailed model documentation
Process state
under review
Model scope and methods
Model documentation: Model scope and methods - IFs
Model type
- Integrated assessment model
- Energy system model
- CGE
- CBA-integrated assessment model
Geographical scope
- Global
- Regional
Solution concept
- Partial equilibrium (price elastic demand)
- Partial equilibrium (fixed demand)
- General equilibrium (closed economy)
Solution horizon
- Recursive dynamic (myopic)
- Intertemporal optimization (foresight)
Solution method
- Simulation
- Optimization
- Dynamic recursive with annual time steps through 2100.
Anticipation
Myopic
Temporal dimension
Base year:2015, time steps:1 year time steps, horizon: 2100
Spatial dimension
Number of regions:186
- Afghanistan
- Albania
- Algeria
- Angola
- Argentina
- Armenia
- Australia
- Austria
- Azerbaijan
- Bahamas
- Bahrain
- Bangladesh
- Barbados
- Belarus
- Belgium
- Belize
- Benin
- Bhutan
- Bolivia
- Bosnia
- Botswana
- Brazil
- Brunei
- Bulgaria
- Burkina Faso
- Burundi
- Cambodia
- Cameroon
- Canada
- Cape Verde
- Central African Republic
- Chad
- Chile
- China
- Colombia
- Comoros
- Congo, Democratic Republic of
- Congo, Republic of
- Costa Rica
- Cote d'Ivoire
- Croatia
- Cuba
- Cyprus
- Czech Republic
- Denmark
- Djibouti
- Dominican Republic
- Ecuador
- Egypt
- El Salvador
- Equatorial Guinea
- Eritrea
- Estonia
- Ethiopia
- Fiji
- Finland
- France
- Gabon
- Gambia
- Georgia
- Germany
- Ghana
- Greece
- Grenada
- Guatemala
- Guinea
- Guinea Bissau
- Guyana
- Haiti
- Honduras
- Hong Kong
- Hungary
- Iceland
- India
- Indonesia
- Iran
- Iraq
- Ireland
- Israel
- Italy
- Jamaica
- Japan
- Jordan
- Kazakhstan
- Kenya
- North Korea
- South Korea
- Kosovo
- Kuwait
- Kyrgyzstan
- Laos
- Latvia
- Lebanon
- Lesotho
- Liberia
- Libya
- Lithuania
- Luxembourg
- Macedonia
- Madagascar
- Malawi
- Malaysia
- Maldives
- Mali
- Malta
- Mauritania
- Mauritius
- Mexico
- Micronesia
- Moldova
- Mongolia
- Montenegro
- Morocco
- Mozambique
- Myanmar
- Namibia
- Nepal
- Netherlands
- New Zealand
- Nicaragua
- Niger
- Nigeria
- Norway
- Oman
- Pakistan
- Palestine
- Panama
- Papua New Guinea
- Paraguay
- Peru
- Philippines
- Poland
- Portugal
- Puerto Rico
- Qatar
- Romania
- Russia
- Rwanda
- Samoa
- Sao Tome and Principe
- Saudi Arabia
- Senegal
- Serbia
- Seychelles
- Sierra Leone
- Singapore
- Slovak Republic
- Slovenia
- Solomon Islands
- Somalia
- South Africa
- Spain
- Sri Lanka
- St. Lucia
- St. Vincent and the Grenadines
- Sudan
- South Sudan
- Suriname
- Swaziland
- Sweden
- Switzerland
- Syria
- Taiwan
- Tajikistan
- Tanzania
- Thailand
- Timor-Leste
- Togo
- Tonga
- Trinidad
- Tunisia
- Turkey
- Turkmenistan
- UAE
- Uganda
- Ukraine
- United Kingdom
- Uruguay
- USA
- Uzbekistan
- Vanuatu
- Venezuela
- Vietnam
- Yemen
- Zambia
- Zimbabwe
Time discounting type
- Discount rate exogenous
- Discount rate endogenous
Policies
- Emission tax
- Emission pricing
- Cap and trade
- Fuel taxes
- Fuel subsidies
- Feed-in-tariff
- Portfolio standard
- Capacity targets
- Emission standards
- Energy efficiency standards
- Agricultural producer subsidies
- Agricultural consumer subsidies
- Land protection
- Pricing carbon stocks
Socio-economic drivers
Model documentation: Socio-economic drivers - IFs
Population
- Yes (exogenous)
- Yes (endogenous)
Population age structure
- Yes (exogenous)
- Yes (endogenous)
Education level
- Yes (exogenous)
- Yes (endogenous)
Urbanization rate
- Yes (exogenous)
- Yes (endogenous)
GDP
- Yes (exogenous)
- Yes (endogenous)
Income distribution
- Yes (exogenous)
- Yes (endogenous)
Employment rate
- Yes (exogenous)
- Yes (endogenous)
Labor productivity
- Yes (exogenous)
- Yes (endogenous)
Total factor productivity
- Yes (exogenous)
- Yes (endogenous)
Autonomous energy efficiency improvements
- Yes (exogenous)
- Yes (endogenous)
Macro-economy
Model documentation: Macro-economy - IFs
Economic sector
Industry
- Yes (physical)
- Yes (economic)
- Yes (physical & economic)
Energy
- Yes (physical)
- Yes (economic)
- Yes (physical & economic)
Transportation
- Yes (physical)
- Yes (economic)
- Yes (physical & economic)
Residential and commercial
- Yes (physical)
- Yes (economic)
- Yes (physical & economic)
Agriculture
- Yes (physical)
- Yes (economic)
- Yes (physical & economic)
Forestry
- Yes (physical)
- Yes (economic)
- Yes (physical & economic)
Other economic sector
- Materials
- Manufactures
- ICT tech
Macro-economy
Trade
- Coal
- Oil
- Gas
- Uranium
- Electricity
- Bioenergy crops
- Food crops
- Capital
- Emissions permits
- Non-energy goods
- Energy
- Agriculture
- Materials
- Manufactures
- Services
- ICT tech
Cost measures
- GDP loss
- Welfare loss
- Consumption loss
- Area under MAC
- Energy system cost mark-up
Categorization by group
- Income
- Urban - rural
- Technology adoption
- Age
- Gender
- Education level
- Household size
Institutional and political factors
- Early retirement of capital allowed
- Interest rates differentiated by country/region
- Regional risk factors included
- Technology costs differentiated by country/region
- Technological change differentiated by country/region
- Behavioural change differentiated by country/region
- Constraints on cross country financial transfers
Resource use
Coal
- Yes (fixed)
- Yes (supply curve)
- Yes (process model)
Conventional Oil
- Yes (fixed)
- Yes (supply curve)
- Yes (process model)
Unconventional Oil
- Yes (fixed)
- Yes (supply curve)
- Yes (process model)
Conventional Gas
- Yes (fixed)
- Yes (supply curve)
- Yes (process model)
Unconventional Gas
- Yes (fixed)
- Yes (supply curve)
- Yes (process model)
Uranium
- Yes (fixed)
- Yes (supply curve)
- Yes (process model)
Bioenergy
- Yes (fixed)
- Yes (supply curve)
- Yes (process model)
Water
- Yes (fixed)
- Yes (supply curve)
- Yes (process model)
Raw Materials
- Yes (fixed)
- Yes (supply curve)
- Yes (process model)
Land
- Yes (fixed)
- Yes (supply curve)
- Yes (process model)
Technological change
Energy conversion technologies
- No technological change
- Exogenous technological change
- Endogenous technological change
Energy End-use
- No technological change
- Exogenous technological change
- Endogenous technological change
Material Use
- No technological change
- Exogenous technological change
- Endogenous technological change
Agriculture (tc)
- No technological change
- Exogenous technological change
- Endogenous technological change
Energy
Model documentation: Energy - IFs
Energy technology substitution
Energy technology choice
- No discrete technology choices
- Logit choice model
- Production function
- Linear choice (lowest cost)
- Lowest cost with adjustment penalties
Energy technology substitutability
- Mostly high substitutability
- Mostly low substitutability
- Mixed high and low substitutability
Energy technology deployment
- Expansion and decline constraints
- System integration constraints
Energy
Electricity technologies
- Coal w/o CCS
- Coal w/ CCS
- Gas w/o CCS
- Gas w/ CCS
- Oil w/o CCS
- Oil w/ CCS
- Bioenergy w/o CCS
- Bioenergy w/ CCS
- Geothermal power
- Nuclear power
- Solar power
- Solar power-central PV
- Solar power-distributed PV
- Solar power-CSP
- Wind power
- Wind power-onshore
- Wind power-offshore
- Hydroelectric power
- Ocean power
Note: Electricity is aggregated for all fuel types in the model.
Hydrogen production
- Coal to hydrogen w/o CCS
- Coal to hydrogen w/ CCS
- Natural gas to hydrogen w/o CCS
- Natural gas to hydrogen w/ CCS
- Oil to hydrogen w/o CCS
- Oil to hydrogen w/ CCS
- Biomass to hydrogen w/o CCS
- Biomass to hydrogen w/ CCS
- Nuclear thermochemical hydrogen
- Solar thermochemical hydrogen
- Electrolysis
Refined liquids
- Coal to liquids w/o CCS
- Coal to liquids w/ CCS
- Gas to liquids w/o CCS
- Gas to liquids w/ CCS
- Bioliquids w/o CCS
- Bioliquids w/ CCS
- Oil refining
Refined gases
- Coal to gas w/o CCS
- Coal to gas w/ CCS
- Oil to gas w/o CCS
- Oil to gas w/ CCS
- Biomass to gas w/o CCS
- Biomass to gas w/ CCS
Heat generation
- Coal heat
- Natural gas heat
- Oil heat
- Biomass heat
- Geothermal heat
- Solarthermal heat
- CHP (coupled heat and power)
Grid Infra Structure
Electricity
- Yes (aggregate)
- Yes (spatially explicit)
Gas
- Yes (aggregate)
- Yes (spatially explicit)
Heat
- Yes (aggregate)
- Yes (spatially explicit)
CO2
- Yes (aggregate)
- Yes (spatially explicit)
Hydrogen
- Yes (aggregate)
- Yes (spatially explicit)
Energy end-use technologies
Passenger transportation
- Passenger trains
- Buses
- Light Duty Vehicles (LDVs)
- Electric LDVs
- Hydrogen LDVs
- Hybrid LDVs
- Gasoline LDVs
- Diesel LDVs
- Passenger aircrafts
Freight transportation
- Freight trains
- Heavy duty vehicles
- Freight aircrafts
- Freight ships
Industry
- Steel production
- Aluminium production
- Cement production
- Petrochemical production
- Paper production
- Plastics production
- Pulp production
Residential and commercial
- Space heating
- Space cooling
- Cooking
- Refrigeration
- Washing
- Lighting
Land-use
Model documentation: Land-use - IFs
Land cover
- Cropland
- Cropland irrigated
- Cropland food crops
- Cropland feed crops
- Cropland energy crops
- Forest
- Managed forest
- Natural forest
- Pasture
- Shrubland
- Built-up area
Agriculture and forestry demands
- Agriculture food
- Agriculture food crops
- Agriculture food livestock
- Agriculture feed
- Agriculture feed crops
- Agriculture feed livestock
- Agriculture non-food
- Agriculture non-food crops
- Agriculture non-food livestock
- Agriculture bioenergy
- Agriculture residues
- Forest industrial roundwood
- Forest fuelwood
- Forest residues
Agricultural commodities
- Wheat
- Rice
- Other coarse grains
- Oilseeds
- Sugar crops
- Ruminant meat
- Non-ruminant meat and eggs
- Dairy products
Emission, climate and impacts
Model documentation: Emissions - IFs, Climate - IFs, Non-climate sustainability dimension - IFs
Greenhouse gases
- CO2 fossil fuels
- CO2 cement
- CO2 land use
- CH4 energy
- CH4 land use
- CH4 other
- N2O energy
- N2O land use
- N2O other
- CFCs
- HFCs
- SF6
- PFCs
Pollutants
- CO energy
- CO land use
- CO other
- NOx energy
- NOx land use
- NOx other
- VOC energy
- VOC land use
- VOC other
- SO2 energy
- SO2 land use
- SO2 other
- BC energy
- BC land use
- BC other
- OC energy
- OC land use
- OC other
- NH3 energy
- NH3 land use
- NH3 other
Climate indicators
- Concentration: CO2
- Concentration: CH4
- Concentration: N2O
- Concentration: Kyoto gases
- Radiative forcing: CO2
- Radiative forcing: CH4
- Radiative forcing: N2O
- Radiative forcing: F-gases
- Radiative forcing: Kyoto gases
- Radiative forcing: aerosols
- Radiative forcing: land albedo
- Radiative forcing: AN3A
- Radiative forcing: total
- Temperature change
- Sea level rise
- Ocean acidification
- Precipitation change
Carbon dioxide removal
- Bioenergy with CCS
- Reforestation
- Afforestation
- Soil carbon enhancement
- Direct air capture
- Enhanced weathering
Climate change impacts
- Agriculture
- Energy supply
- Energy demand
- Economic output
- Built capital
- Inequality
Co-Linkages
- Energy security: Fossil fuel imports & exports (region)
- Energy access: Household energy consumption
- Air pollution & health: Source-based aerosol emissions
- Air pollution & health: Health impacts of air Pollution
- Food access
- Water availability
- Biodiversity
Model Documentation - IFs
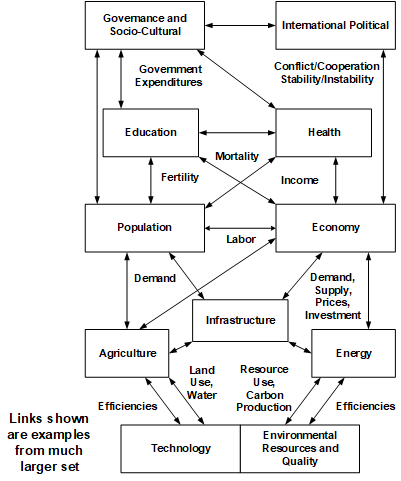
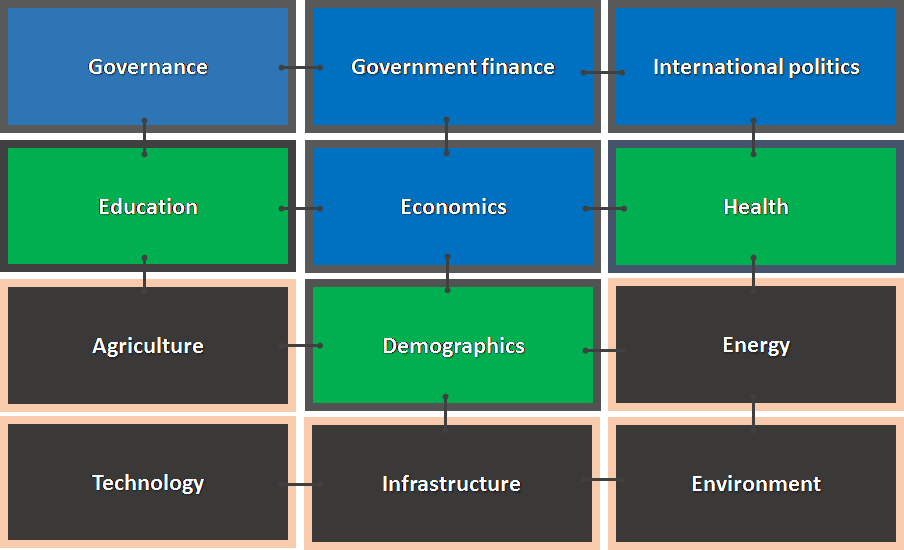
International Futures (IFs) is a long-term integrated assessment model or system which is a collection of several hard–linked, directly interconnected models (sometimes referred to as modules). It is dynamic recursive with annual time steps to 2100. It represents 186 countries connected through a variety of flows, facilitates aggregation of them to global regions, and allows subdivision of them into more local socio-political units. The IFs system is available for use by others both on-line and in a downloadable version, and it is open source. Major models in IFs (see Figure below) include
- a multistate population model (which represents 22 age sex cohorts to age 100+ and differentiates their educational attainment and cause-specific mortality patterns).
- a multisector general equilibrium economic model (which uses inventories as buffer stocks and to provide price signals so that the model chases equilibrium over time); it provides labor, investment, and consumption information to partial equilibrium energy and agriculture models.
- an education model that tracks grade-by-grade student progression and aging of adults with variable attainment levels.
- a health model that represents age-sex specific mortality and morbidly by 15 causes of death.
- socio-political representations that include governance capacity and finance, wrapping the economic model in a broader social accounting matrix.
- an energy model (which portrays production of six energy types: oil, gas, coal, nuclear, hydroelectric, and other renewable). Physical values from the partial equilibrium model are converted to currency values to replace those in the general equilibrium economic model.
- an agricultural model (which is a partial equilibrium model in which food stocks buffer imbalances between production and consumption and determine price changes); the model represents crop, gazing, forest, developed and other land. As with energy, physical values converted to monetary values override those in the general equilibrium model.
- an infrastructure model that projects paved roads, access to safe water and sanitation, electricity access, and access to various forms of information and communications technology,
- an environmental model, which allows tracking of remaining resources of fossil fuels, area of forested land, water supply-demand, atmospheric carbon dioxide, and changes in temperature and precipitation.
- an implicit technology model, which allows changes in assumptions about rates of technological advance in health, agriculture, energy, and the broader economy.
1) Model scope and methods - IFs
International Futures (IFs) is an interactive tool for the exploration of the long-term future of closely interacting and dynamically hard-linked issue clusters, namely human development, social change, and environmental sustainability. Among other applications, IFs facilitates scenario analysis across a wide range of the Sustainable Development Goals.
1.1) Model concept, solver and details - IFs
International Futures (IFs) is a large-scale, long-term, integrated global modeling system. The system is dynamic recursive with 1-year time steps through 2100.
IFs is a tool for thinking about long-term global trends and strategic planning for the future. Among the unique features of the system is the extensive integration of models across human capacity, social, and natural systems. IFs contains highly integrated (hard-linked) models across demographic, economic, education, health, governance, agriculture, energy, infrastructure, water, climate and other subsystems for 186 countries interacting in the global system. The central purpose of IFs is to facilitate exploration of global futures through alternative scenarios.
IFs can help a user
- Understand the state of major global systems
- Explore long-term trends and consider where they might take us
- Learn about the dynamic interactions across global subsystems
- Clarify long-term organizational goals/priorities
- Develop alternative scenarios (if-then statements) about the future
- Investigate how different agent categories (households, firms and governments) can shape the future
IFs is integrated with a large database (more than 4,000 series) for its countries, most of which include data since 1960. The system is fully imbedded in an interactive interface, and it is both open source and freely available to users both on-line (www.ifs.du.edu) and in downloadable form. The interface facilitates data analysis, projection exploration and comparison, and flexible scenario analysis. The models of IFs and their interactions. Figure 1 shows the major hard-linked models within the IFs system.
The multistate demographic model uses a standard cohort-component representation. Fertility and mortality are endogenous in response to other drivers, including adult educational attainment from a full education model and 15 categories of mortality and morbidity from a health model. In the education model students flow by grade through primary, lower secondary upper secondary, and tertiary levels. In the health model, mortality and morbidity are age and sex specific.
The multisector economic model is general equilibrium, although the model uses changes in inventory stocks and relative prices to drive changes in supply and demand, chasing equilibrium over time rather than solving for it or iterating to it in every time cycle. This is consistent with actual market behavior and facilitates computational efficiency. The partial equilibrium physical agriculture model differentiates crop, meat and fish and generates calorie and protein availability. The partial equilibrium energy model differentiates coal, oil, natural gas, hydroelectric power, nuclear power, and renewable energy, tracking resources bases and production. Key variables from the agriculture and energy models, converted to monetary terms, override those of the same sectors in the economic model, while the integration across sectors in the economic model of variables including household, government and firm demand and savings/investment availability provide information to and constraints upon the physical models.
There are also water and infrastructure models. The water model represents supply from renewable and nonrenewable sources and demand for agricultural, municipal and industrial uses. Agricultural water use is linked to irrigation in the agriculture model and can constrain yields. The infrastructure model represents extent of and access to paved roads, safe water and sanitation, electricity, and information and communication technologies. It requires investment from public and private sectors that compete with demand from the education and health models, as well as other uses.
The physical agriculture and energy models determine land use and generate carbon emissions. A representation based on the MAGICC model, used widely in IAMs. connects carbon emissions to atmospheric levels, global warming, and country-level changes in temperature and precipitation. Those feed forward to the agriculture model with a mixture of potentially positive and negative consequences.
Across the broader IFs system, two aspects are especially important in the interaction of all of the separate models. The first is finance, including governmental revenues and expenditures, but also those of households and firms. The economic system is imbedded within a full social accounting matrix that represents all financial flows within and across these agent categories and assures that representation of those flows is appropriately balanced and constrained—there are thus no free lunches. The second area where systems are highly interactive is via the endogenous representation of productivity in the economic model. Multifactor productivity is responsive to changes in human capital (education and health), social capital (including governance quality), physical capital (including infrastructure development), and knowledge capital (including research and development spending but also the knowledge imbedded in trade among countries).
A broader model of governance represents the state of domestic security or instability, corruption, and inclusion (democracy) and connects to government finance. Socio-political variables also trace change in basic value/cultural structures, and portray various elements of formal and informal socio-economic structures and processes, including income distribution. The IFs system also represents changes in country power positions globally, a foundation of international politics and potentially of capability for collective global action.
Technological change is important across most of the models in IFs. While exogenously represented in many instances, the production functions in the economic, agriculture, and energy models have elements of learning by doing. This brief summary only touches on the model structure and interconnections; for more extensive coverage see Hughes (2019 forthcoming) and the IFs project Wiki (http://pardee.du.edu/wiki/Main_Page).
The interactive interface of IFs and analysis with the system. Because IFs is dynamic recursive and computationally efficient, scenario development and exploration with it can be interactive. The completion of a single run with the system requires less than 15 minutes on a fast laptop or the project’s own server, where it is available also for use by others. Figure 2 shows the main screen for interaction with the system. Leaving aside Extended Features (which the IFs Wiki also documents), there are three major functionalities in the main menu, each of which lead into a large number of sub-options:
- Data analysis. This functionality allows interaction with the more than 4,000 data series packaged with IFs, including display on maps as well as both displays and statistical exploration longitudinally and in cross-sectional analysis.
- Display. This functionality facilitates standard graphical and tabular representations from the Base Case and other scenarios of IFs, using any combination of individual countries or country groupings. At the most detailed level, one form of display (Self-Managed) can call up any variable or parameter in the system. There is also a very extensive set of prepackaged displays described in natural language that contain most of the variables in the model individually or in combination, often in combination with historical series for the same variable(s). In addition, the Display functionality includes a wide selection of specialized displays including age-sex population graphics for population alone or overlaid with educational attainment or mortality rates, analysis of contributions of multiple drivers of economic growth, and both overview and drill down capability on a wide range of indicators across the Sustainable Development Goals.
- Scenario analysis. This functionality provides access to all parameters and initial conditions in IFs. For temporally specific parameter changes, it supports interpolation or even year-by-year specification. Users can save collections of parameter changes into scenario specification files for further future editing and can use the specification files at any time to create scenario run files for analysis and comparison via the display functionality. A large library of saved scenario specification files exists for users, including representation of the Shared Socioeconomic Pathways (SSPs)
1.3) Temporal dimension - IFs
Future-Oriented Analysis. The base year of IFs is 2015 and the model runs recursively in annual time steps through horizons up to 2100. The interface has a stop and start capability to facilitate scenario analysis. The base year is changed fairly often as new data releases allow; a data “preprocessor” includes algorithms to clean and reconcile data series so as to facilitate data and base year updates.
Historical Analysis. IFs also includes an extensive and growing historical data base (over 4000 series) starting in 1960. The data base allows initiation of model runs in 1960 and comparison of projections with empirical values.
1.4) Spatial dimension - IFs
Countries. There are 186 countries in the IFs database and model system.
Groups. The IFs interface can aggregate projections across countries into country groupings using variable-specific rules (including sums and various weighted averages); the interface includes a great many standard country groupings as identified by different international organizations. The user can create additional groupings.
Country sub-units. The ability to split countries down into smaller geopolitical entities (provinces, districts, states, etc.) is available for all countries and has been developed with data support in various projects for selected countries.
G-Lists. For ease of result presentation users can define lists of countries, groups, and country sub-units for analysis; many have been pre-defined.
1.5) Policy - IFs
All model parameters and initial conditions are accessible via the interlace and therefore changeable by users. Example areas where policy interventions can be introduced into the model are
- Demographics: fertility, mortality (in more detail via the health model), and migration—all of which affect population growth and level.
- Economics: on the production side are investment, labor force participation, and productivity (via assumptions about systemic advance, convergence rate, and a wide range of specific endogenous drivers); interventions are also possible on savings levels and consumption patterns and on patterns of trade.
- Education: enrollment, continuation, and completion/transition rates; spending levels.
- Health: mortality and morbidity rates across 15 different causes.
- government revenue and expenditure patterns from multiple sources and to multiple targets; corruption and democracy levels; status of women; value change.
- Geopolitics: Country and regional power levels.
- Food and Agriculture: Land use and yield/production levels; trade patterns—all of which affect calorie availability and malnutrition rates.
- Energy: Resource and production level by energy type including renewable energy share, demand level and patterns.
- Infrastructure: investment and access extension by type (road, water, sanitation, electricity, ICT).
- Environment: atmospheric carbon dioxide levels via interventions in models noted above (e.g. land use, carbon intensity of energy); water demand by final use and water supply by source.
Prepackaged scenario intervention files also allow integrated analysis of scenario sets including the UNEP GEO-4 set and the Shared Socioeconomic Pathway (SSP) set.
2) Socio-economic drivers - IFs
In forecasting long-term change, it is useful to distinguish distal and proximate drivers. The former consist of driving variables that help account for long-term structural change. They may operate at some causal distance from the variable we are forecasting, but we know them to be deeply structurally related to that variable, often via multiple paths. On the other hand, proximate variables are those that create shorter-term variation, often in part as intermediate variables between the deeper or distal drivers and the target variable, but often also as levers that policy or other short-term factors may influence somewhat independently of the deeper drivers. Key formulations across the models of IFs generally involve a combination of distal and proximate drivers.
The common approach across other IAMs represented in this ADVANCE project-based Wiki is to use this section to discuss the representation of population and economic activity (exogenously or endogenously) as drivers for the biophysical systems that other Wiki sections then elaborate. However, the IFs system contains a variety of models (see Model scope and methods/Model concept, solver and details) that require some elaboration here. These models are not only drivers, but driven subsystems of IFs, responding to each other and to change in biophysical systems. In keeping with the structure of this Wiki, we will save discussion of the energy model for another top-level topic and similarly elaborate the economic model in its own topic. But in addition to population and an introductory survey of economy activity, we will also provide subtopics here on the IFs models of education, health, governance, infrastructure, interstate politics, and socio-political variables.
2.1) Population - IFs
The dominant population equation is a simple addition of births (BIRTHS) at the bottom of the cohort distribution, subtraction of deaths (DEATHS) from each population cohort, and advance of people to the next cohort over time. Although the output from IFs shows population in the standard 5-year age categories, the model maintains single-year categories internally to be consistent with its one-year time steps, thereby avoiding numerical diffusion of changes to the bottom of 5-year categories to higher age categories.
Births are most immediately a function of the total fertility rate (TFR), which in the longer term responds especially to education level of the adult population, infant mortality rates, and contraception usage rates. The model user has direct control over TFR with a multiplier and for low fertility countries with a parameter specifying long-term stabilization level for fertility.
Deaths are primarily a function of age-sex specific mortality rates computed within the IFs health model where they respond in the long run to adult education and also to GDP per capita and technology change, as well as mortality cause specific proximate drivers (e.g. indoor (solid fuel related) or urban air pollution). The model user has direct control over all deaths with a mortality multiplier and over those specific to a cause of health with an alternative mortality multiplier
2.2) Economic activity - IFs
The economic model (elaborated in the Macro-economy topic) produces GDP at market exchange rates and at purchasing power parity. It also produces value added, consumption, and trade in each of six economic sectors: agriculture, primary energy, raw materials, manufactures, services, and information/communications technology. It further provides a calculation of income distribution in the form of a Gini index.
Two features of the economic model are notable. First, it is embedded in a full social accounting matrix (SAM) structure, thereby assuring consistency of financial flows among firms, households, and government. Second, the production function, fundamentally important to long-term dynamics, includes endogenous representation of multifactor productivity, driving it by changes in human, social, and physical capital from other models, as well as knowledge advance. Both the SAM and the production function are therefore pivot points for the interaction of dynamics across the range of models in the integrated IFs system.
On the forward linkage side, GDP per capita is one of the key distal or deep developmental drivers that affects many other variables across the models of the IFs system. Most often, GDP per capita at purchasing power parity (PPP) is the variable used. See other IFs models for details of its impact.
3) Macro-economy - IFs
The economic model represents supply, demand, and trade in each of six economic sectors: agriculture, primary energy, raw materials, manufactures, services, and information/communications technology. The model draws upon data from many sources including the Global Trade and Analysis Project (GTAP) with 57 sectors as of GTAP 8; the IFs pre-processor (integrated software that reads raw data and prepares the initial base year for all models) collapses those into the six IFs sectors and theoretically could collapse them into a different aggregated subset. On the supply side, a Cobb-Douglas production function determines value added. Thus two principal factors are capital and labor. Labor is responsive not just to population size and structure, but to the labor participation rate, including the changing role of women in the work force. A labor submodel calculates labor demand that is equilibrated over time with supply, but allows unemployment rate changes. Accumulated growth in the level of technology or multifactor productivity (MFP), in a "disembodied" representation (TEFF), modifies these factors. Immediate energy shortages/shocks can also affect value added.
The technological factor in the production function is often called multifactor productivity (MFP). The basic value of MFP is a sum of a global productivity growth rate driven by the economically advanced or leading country/region, a technological convergence factor dependent on GDP per capita, and an exogenous or scenario factor. In addition, however, other factors affect productivity growth over time. These include a wide range of variables across human, social, physical, and knowledge capital categories. For instance, years of adult education attainment and the level of economic freedom, respectively are among the variables that affect change in MFP associated with human and social capital.
Input-output matrices, which are tied to GTAP data but specified dependent on the level of development (GDP per capita), allow the computation from value added of gross production. The calculation of gross production (ZS) in value terms within the economic model is overridden by calculations of physical production converted to value in the agricultural and energy models when respective switches (AGON and ENON) are thrown as in the default of the IFs Base Case scenario. After satisfaction of intersectoral flows, the remainder of gross production is available for meeting final demand, both domestic and in other countries via trade.
On the demand side, most of household income supports consumption, which is directed to sectors via a linear expenditure system. It is the balance of this production for final demand with actual final demand that determines whether inventories grow or decline. Inventories (or stocks) are the key equilibrating variable in four negative or equilibrating feedback loops. As inventories rise, prices fall, increasing final demand (one loop), decreasing production (a second loop), and thereby in total decreasing inventories in the pursuit over time of a target value and equilibrium. Similarly, as inventories rise, capacity utilization falls, decreasing production, and restraining inventories. Finally, relative prices affect the levels of trade among countries.
In the longer run, investment and capital stocks are the key driving variables in an important positive feedback loop. As capital rises, it increases value added and GDP, increasing final demand and further increasing investment. Capital stock is a function of investment and depreciation rates. Endogenously determined investment can be influenced exogenously by a multiplier and the lifetime of capital can be changed. Similarly, government social investment can increase productivity, production and inventories in another positive feedback loop.
4) Energy - IFs
Energy demand in IFs is most immediately a function of GDP and the energy demand per unit of GDP. Energy production is most immediately a function of capital stock in each energy type, the capital/output ratio for that energy type, and a capacity utilization factor.
Energy demand per unit of GDP depends on GDP per capita, energy prices, and an autonomous trend in energy efficiency. The first two of these are computed endogenously, the latter is provided exogenously. The user can control the price elasticity of energy demand and the autonomous trend in efficiency of energy use. The user can also use an energy demand multiplier to directly modify energy demand.
For fossils fuels and hydro, there are upper bounds on production. For fossil fuels, these are based on reserve production ratios, as well as user-specified upper bounds. For hydro, the upper bound relates to hydropower potential. The model user can also control production using an energy demand multiplier to directly modify energy production by energy type.
The capital/output (capital/production) ratios for all fuel types decline over time due to technological improvements at rates determined by two user controllable parameters. For fossil fuels, this is counteracted by a factor that increases the capital/output ratio as the amount of remaining resources decreases. Something similar happens for hydro and other renewables, but here the capital/output ratios increase as production approaches a maximum possible level. The user can further modify the capital/output ratios with the multipliers.
Energy capital, by fuel type, is initialized based on the initial levels of production and capital/output ratios. Energy capital depreciates at a rate determined by the lifetime of energy capital and it grows with investment. Total desired investment in energy capital is influenced by many factors, including existing capital, domestic and global energy demand, the production of other renewables, changes in the global capital/output ratio, world and domestic energy stocks, expected overall profits in the energy sector, and imports. Users can influence this in the aggregate and can also control the effect of expected profits and world energy stocks. Desired investment by energy type increases with individual profit expectations, but also by limits related to reserve production factors (for fossil fuels and hydro), any exogenous restrictions on maximum production (for fossil fuels), ultimate potential (for hydro), and other, unspecified factors (nuclear). Users can influence the effect of profit expectations by fuel type as well as influence the desired investment by energy type in the aggregate. The user can also specify an exogenous growth rate for energy investment by fuel type. The economic model ultimately determines whether all of the investment needs can be met; in case of shortfalls, the investment in each type of energy is reduced proportionately.
IFs separately represents ultimate resources and known reserves, where the latter are the amount of energy resources available to be produced. Resources and reserves, both conventional and unconventional, are set in the pre-processor. The user can modify the default assumptions on ultimate resources, either directly or via the use of multipliers. Reserves decline with production and increase with discoveries. The rate of discovery depends on the ultimate resources remaining, the intensity of current production, world energy prices, and a base rate of discovery. The user can control the effect of world prices on discovery, augment the base rate of discovery, and use a multiplier to affect the rates of discovery. Finally, IFs keeps track of any production not used in the current year, i.e., stocks, and shortages.
Domestic energy prices are influenced by world stocks, domestic stocks, and the ratio of capital to production at the global level. The user can control the effect of domestic stocks on prices. Users can also include a “cartel premium” and a carbon tax. More directly users can set domestic energy prices exogenously for just the first year or for multiple future years. The world energy price is calculated as a weighted sum of the domestic prices.
The energy model also provides representation and control over energy trade. The levels of imports and exports depend upon levels of production and demand, as well as past propensities to import and export energy. The user can set maximum limits on of energy imports and energy exports, as well as general limits on trade.
4.1) Energy resource endowments - IFs
4.1.1) Fossil energy resources - IFs
For fossils fuels and hydro, there are upper bounds on production. For fossil fuels, these are based on reserve production ratios, as well as user-specified upper bounds. For hydro, the upper bound relates to hydropower potential. The model user can also control production using an energy demand multiplier to directly modify energy production by energy type.
4.1.2) Uranium and other fissile resources - IFs
4.1.3) Bioenergy - IFs
4.1.4) Non-biomass renewables - IFs
4.2) Energy conversion - IFs
4.2.1) Electricity - IFs
4.2.2) Heat - IFs
4.2.3) Gaseous fuels - IFs
4.2.4) Liquid fuels - IFs
4.2.5) Solid fuels - IFs
4.2.6) Grid, pipelines and other infrastructure - IFs
4.3) Energy end-use - IFs
4.3.1) Transport - IFs
4.3.2) Residential and commercial sectors - IFs
4.3.3) Industrial sector - IFs
4.3.4) Other end-use - IFs
4.4) Energy demand - IFs
Energy demand in IFs is most immediately a function of GDP and the energy demand per unit of GDP. Energy demand per unit of GDP depends on GDP per capita, energy prices, and an autonomous trend in energy efficiency. The first two of these are computed endogenously, the latter is provided exogenously. The user can control the price elasticity of energy demand and the autonomous trend in efficiency of energy use. The user can also use an energy demand multiplier to directly modify energy demand.
4.5) Technological change in energy - IFs
5) Land-use - IFs
In the IFs model, land is divided into 5 categories: crop land, grazing land, forest land, ’other’ land, and urban or built-up land. First, changes in urban land are driven by changes in average income and population, and draw from all other land types. Second, the investment in cropland development is the primary driver of changes in cropland, with shifts being compensated by changes in forest and "other" land. Third, changes in grazing land are a function of average income (reflecting meat demand), with shifts again being compensated by changes in forest and "other" land. Finally, conservation policies can influence the amount of forest land, with any necessary adjustments coming from crop and grazing land.
5.1) Agriculture - IFs
The agriculture/food model represents crops, meat, and fish production, consumption, and trade in the aggregate, Agricultural production is a function of the availability of resources, e.g. land, livestock, capital, and labor, as well as climate factors and technology. Crop yield is a function of technology, capital, and labor. It is differentiated between irrigated and non-irrigated land. It is posited to have upper limits and to be responsive to stocks/inventories.
The model also accounts for lost production (such as spoilage in the fields or in the first stages of the food supply chain), distribution and transformation losses, and consumption losses, which are responsive to average income. Income levels are the primary drivers of caloric demand, which then determines food demand taking into account country-specific differences than can reflect income and cultural differences. The model distinguishes crop demand for food, animal feed, and industrial usage. Stocks or inventories (or relative prices in different model versions) provide feedback to supply and demand sides of the model.
Stocks and stock changes also play a role in driving the model’s demand for agricultural investment. The actual levels of investment are finalized in the economic model of IFs and subject to constraints there. The investment can be of two types – investment for expanding and maintaining cropland (extensification) and investment for increasing crop yields per unit area (intensification). The expected relative rates of return determine the split.
The final key dynamics addressed in the agriculture model relate to land, livestock, and water. The latter of these is very straightforward, driven only by crop production. Changes in livestock herd size are influenced by changes in the demand for meat, but also by changes in available grazing land, and the ability of countries to import.
6) Emissions - IFs
Fossil fuel consumption generates carbon emissions specific to coal, oil, and natural gas use. Net deforestation generates additional carbon emissions or removal. IFs does not represent other greenhouse gas emissions. The model exogenously represents net removals from the atmosphere by ocean and land sinks and traces resultant level of atmospheric carbon. See topics on the energy and agriculture models for discussion of formulations and of control parameters.
6.1) GHGs - IFs
6.2) Pollutants and non-GHG forcing agents - IFs
6.3) Carbon dioxide removal (CDR) options - IFs
7) Climate - IFs
8) Non-climate sustainability dimension - IFs
The non-climate sustainability dimension of IFs is mostly focused on water (see documentation page for water). There are also many other models within IFs not fully documented here such as: Education, Governance, Health, Infrastructure, Interstate Politics, and Socio-Political. There are brief descriptions of each of these models in the documentation page for "Other materials."
8.2) Water - IFs
IFs represents water demand as the sum of the demand of three sectors—municipal, industrial (differentiating energy-related from other industrial demand), and agriculture. The data from AQUASTAT differentiates between these three sectors and many other water models represent these same sectors. AQUASTAT refers to these data series as “water withdrawal.” IFs treats water withdrawal as equivalent to water demand.
Water supply is defined as the sum of five components: surface water withdrawal, renewable groundwater withdrawal, non-renewable (fossil) water withdrawal, desalinated water, and direct use of treated wastewater.
The size of a country’s urban population and water use per capita for the urban population drive municipal water demand. Water use per capita for the urban population is driven by GDP per capita (at purchasing power parity), the portion of the population with access to piped water, and the portion of the population that lives in urban areas. Non-renewable electricity generation capacity and the overall size of a country’s manufacturing sector drive industrial water demand. The area of land under irrigation drives agricultural water demand. The shadow price index impacts all three water demand sectors.
Surface and (renewable) groundwater withdrawals are driven by the shadow price index and constrained by their country-specific exploitable limits. Estimated stocks constrain fossil water withdrawals. The price index and an initial growth rate (which can be altered by user) drive change in desalinated water. Direct use of treated wastewater is driven by the price index and the volume of wastewater which is treated. Total water demand and total water supply are used to adjust the price index. The water price index then impacts each sector of demand and most sources of supply the following year. This algorithmic logic keeps water demand and water supply in approximate equilibrium over time, even though it does not require exact equality in any time step.
Water available for agriculture in this equilibrating process affects both the efficiency of water use and the extent of irrigated land. The latter affects yield in the agricultural model.
8.3) Other materials - IFs
Education
The model forecasts gender- and country-specific access, participation and progression rates at levels of formal education starting from elementary through lower and upper secondary to tertiary. The model also forecasts costs and public spending by level of education. Dropout, completion and transition to the next level of schooling are all mapped onto corresponding age cohorts thus allowing the model to project educational attainment for the entire population at any point in time within the analysis horizon.
From simple accounting of the grade progressions to complex budget balancing and budget impact algorithm, the model draws upon the extant understanding and standards (e.g., UNESCO's ISCED classification) about national systems of education around the world. One difference between other attempts at projecting educational participation and attainment and that of IFs is the embedding of education within an integrated model in which demographic and economic variables interact with education, in both directions, as the model runs.
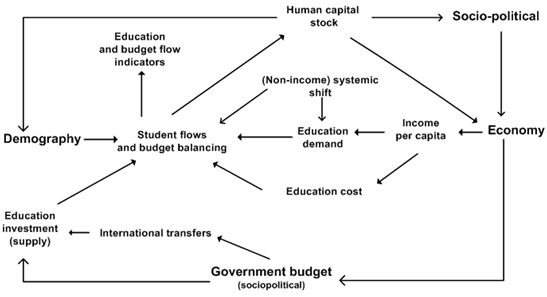
Figure 1 (above) displays the major variables and components that directly determine education demand, supply, and flows in the IFs system. We emphasize again the inter-connectedness of the components and their relationship to the broader human development system. For example, during each year of simulation, the IFs cohort-specific demographic model provides the school age population to the education model. In turn, the education model feeds its calculations of education attainment to the population model’s determination of women’s fertility. Similarly, the broader economic and socio-political systems provide funding for education, and levels of educational attainment affect economic productivity and growth, and therefore also education spending.
Governance
Governance is the two-way interaction between government and the broader socio-political or, even more broadly, socio-cultural system. The conceptual foundation for the representation of governance in IFs owes much to an analysis of the evolution of governance in countries around the world over several centuries. That analysis (see Chapter 1 of the Strengthening Governance Globally volume by Hughes et al. 2014) identified three dimensions of governance: security, capacity, and inclusion. It traced them over time and noted their largely sequential unfolding for currently developed countries and their currently more nearly simultaneous progression in many lower-income countries.
The three dimensions interact closely and bi-directionally with each other. They also interact bi-directionally with broader human development systems. The level of well-being, often captured quantitatively by GDP per capita or the more inclusive human development index, may be especially important, but is hardly alone in helping drive forward advance in governance; for instance, the age structures of populations and economic structures also interact with governance patterns.
The conceptualization of governance further divides each of the three primary dimensions into two sub-dimensions partly based on the desire to quantify them historically and to facilitate scenario analysis. For security those are the probability of intrastate conflict and the general level of country performance and risk. The two sub-dimensions of capacity are the ability to raise revenue and the effective use of it and the other tools of government—that is, the competence or quality of governance. IFs uses corruption (that is, control of it) as a proxy for such competence. The first sub-dimension of inclusion is the level of formal democratization, typically assessed in terms of competitive elections. More broadly democratization involves inclusion of population groupings across lines such as ethnicity, religion, sex, and age; IFs uses gender equity as a proxy for the second dimension.
Health
Health analysis systems typically can help us either (1) to understand better where broad, long-term patterns of human development appear to be taking us with respect to global health, or (2) to consider opportunities for intervention and achievement of alternative health futures, enhancing the foundation for decisions and actions that improve health.
Broad structural models with deep distal drivers such as technological and income advance (e.g., that of the Global Burden of Disease or GBD) assist in the first purpose by relating those distal development drivers to longer-term pattern change in health. Distal driver formulations tend to produce forecasts of constantly decreasing death rates. Yet we know, for instance, that some more proximate factors driving mortality, such as smoking, obesity, and road traffic accidents, tend to increase in developing societies with income and education, before at least smoking and road traffic deaths (and perhaps also obesity) typically decline. The inclusion of such proximate drivers thus opens the door to the second, allowing for consideration of interventions in the pursuit of alternate health futures. A hybrid and integrated model form like that of IFs can help with both purposes and provide a richer overall picture of alternative health futures.
The integrated nature of the IFs modeling system further allows us to think about feedback loops between health outcomes and larger development variables such as economic progress and population structure.
Infrastructure
The dominant relations in the Infrastructure model are those that determine the expected levels of infrastructure stocks and access, spending on infrastructure, and the impacts of infrastructure on health and productivity. The expected levels of infrastructure stocks and access are influenced by socio-economic factors related to population, economic activity, governance, and educational attainment—and, of course, spending on construction and maintenance. In almost every case there are also path dependencies that supplement the basic relationships, reflecting the considerable inertia in infrastructure development.
Spending on infrastructure is divided into private and public spending, with the latter further divided in IFs into ‘core’ and ‘other’ infrastructure. ‘Core’ infrastructure refers to those types of infrastructure that are explicitly represented in the model; ‘other’ infrastructure refers to those types of infrastructure that are not explicitly represented in the model. In IFs, public spending on core infrastructure is driven by the required spending to meet the expected levels of infrastructure stocks and access, constrained by total government consumption and the demands for government consumption in other categories (e.g. education and health). Public spending on other infrastructure is driven by average GDP per capita, total government consumption, and the demands on government consumption from other categories. Deficits and surpluses of government funds will affect the actual levels of funds allocated for both core and other infrastructure. The public spending on core infrastructure leverages a proportionate amount of private spending on core infrastructure, with the amount leveraged depending upon historical relationships found in the literature, which normally reflect the variation in public and private returns between particular types of infrastructure. Finally, in recognition of the incremental approaches that public budgeting decisions usually follow, IFs avoids unusually sharp increases in public spending on infrastructure by smoothing it over time.
Infrastructure development directly affects multifactor productivity, with this effect being treated separately for non-ICT and ICT related infrastructure. The use of solid fuels in the home and access to improved water and sanitation directly affect human health through their effects on the mortality and morbidity rates of specific diseases—diarrheal diseases, acute respiratory infections, and respiratory diseases.
Interstate Politics
Threat of conflict among sates states is a function of many determinants. For instance, contiguity or physical proximity creates contact and therefore the potential for both threat and peaceful interaction. Cultural similarities and differences affect threat levels. Yet certain factors are more subject to rapid change over time than are contiguity or culture. Among factors that change, the relative power of states and their level of democratization substantially affect levels of conflict threat.
Power is a function of population, GDP, technology, and conventional and nuclear military expenditures, in an aggregation with weights that the user can change. IFs computes a power indicator that shows each actor’s portion of global power. It does so by weighting each actor’s share of global GDP (at exchange rates or purchasing power parity), population, a measure of technological sophistication (with GDP per capita as a proxy), government size, military spending, conventional power, and nuclear power. Weights of one "1" add the term to the power calculation, and of “0” remove the term from power calculation.
Democratization is computed in the domestic socio-political model.
Socio-political
Social and political change occurs on three dimensions (social characteristics or individual life conditions, values, and socio-political institutions/process). Although GDP per capita is strongly correlated with all dimensions of change, it might be more appropriate to conceptualize a syndrome or complex of developmental change than to portray an economically-driven process.
The model computes some key social characteristics/life conditions, including life expectancy and fertility rates in the demographic model, but the user can affect them via multipliers. Literacy rate is an endogenous function of education spending, which the user can influence. Building on such variables, IFs provides aggregated indicators of the physical quality of life and the human development index.
The model computes value or cultural change on three dimensions identified by the global World Values Survey project: traditional versus secular-rational, survival versus self-expression, and modernism versus postmodernism, which the user can affect via additive factors.
With respect to socio-political institutions/process, the model endogenously projects freedom, democracy, autocracy, economic freedom, and the status of women. All can be shifted by the user via multipliers.
The larger socio-political model provides representation and control over government spending on education, health, the military, R&D, infrastructure, foreign aid, and a residual category. Military spending is linked to interstate politics, both as a driver of threat and as a result of action-and-reaction based arms spending.
10) References - IFs
Birkmann, Joern, Susan L. Cutter, Dale S. Rothman, Torsten Welle, Matthias Garschagen, Bas van Ruijven, et al. 2013. "Scenarios for Vulnerability: Opportunities and Constraints in the Context of Climate Change and Disaster Risk.” Climatic Change 133(1): 53–68. DOI: 10.1007/s10584-013-0913-2.
Burt, Alison, Barry B. Hughes, and Gary Milante. 2014. “Eradicating Poverty in Fragile States: Prospects of Reaching the ‘High-Hanging’ Fruit by 2030.” WB Policy Research Working Paper no. 7002. World Bank, Washington, DC. http://documents.worldbank.org/curated/en/2014/08/20040315/eradicating-poverty-fragile-states-prospects-reaching-high-hanging-fruit-2030.
Dickson, Janet R., Barry B. Hughes, and Mohammod T. Irfan. 2010. Advancing Global Education. Vol. 2 of the Patterns of Potential Human Progress series. Boulder, CO, and New Delhi, India: Paradigm Publishers and Oxford University Press.
Hillebrand, Evan E., and Stacy Closson. 2015. Energy, Economic Growth, and Geopolitical Futures. Cambridge, MA: MIT Press.
Hughes, Barry B., ed. 2013a. "Development-Oriented Policies and Alternative Human Development Paths: Aggressive but Reasonable Interventions." Prepared by the Frederick S. Pardee Center for International Futures. UNDP Occasional Paper 2013/05. Human Development Report Office, United Nations Development Programme, New York, NY. http://hdr.undp.org/sites/default/files/hdro_1305_pardee.pdf.
Hughes, Barry B. 2016. “International Futures (IFs) and Integrated, Long-Term Forecasting of Global Transformations.” Futures 81(August): 98–118. DOI: 10.1016/j.futures.2015.07.007.
Hughes, Barry B. forthcoming 2019. Exploring and Understanding International Futures: Building a Global Modeling System. Amsterdam: Elsevier.
Hughes, Barry B., David Bohl, Mohammod Irfan, Eli Margolese-Malin, and José R. Solórzano. 2016. “ICT/Cyber Benefits and Costs: Reconciling Competing Perspectives on the Current and Future Balance.” Technological Forecasting and Social Change 115(February): 117–130. DOI: 10.1016/j.techfore.2016.09.027.
Hughes, Barry B., and Evan E. Hillebrand. 2006. Exploring and Shaping International Futures. Boulder, CO: Paradigm.
Hughes, Barry B., Mohammod T. Irfan, Haider Khan, Krishna B. Kumar, Dale S. Rothman, and José R. Solórzano. 2009. Reducing Global Poverty. Vol. 1 of the Patterns of Potential Human Progress series. Boulder, CO, and New Delhi, India: Paradigm Publishers and Oxford University Press.
Hughes, Barry B., Mohammod T. Irfan, Jonathan D. Moyer, Dale S. Rothman, and José R. Solórzano. 2011. "Forecasting the Impacts of Environmental Constraints on Human Development." Human Development Research Paper 2011/08. United Nations Development Programme, New York, NY. http://hdr.undp.org/sites/default/files/hdrp_2011_08.pdf.
Hughes, Barry B., Mohammod T. Irfan, Jonathan D. Moyer, Dale S. Rothman, and José R. Solórzano. 2012. "Exploring Future Impacts of Environmental Constraints on Human Development." Sustainability 4(5): 958–994. DOI: 10.3390/su4050958.
Hughes, Barry B., and Peter D. Johnston. 2005. “Sustainable Futures: Policies for Global Development.” Futures 37(8): 813–831. DOI: 10.1016/j.futures.2005.01.017.
Hughes, Barry B., Devin K. Joshi, Jonathan D. Moyer, Timothy D. Sisk, and José R. Solórzano. 2014. Strengthening Governance Globally. Vol. 5 of the Patterns of Potential Human Progress series. Boulder, CO, and New Delhi, India: Paradigm Publishers and Oxford University Press.
Hughes, Barry B., Randall Kuhn, Cecilia M. Peterson, Dale S. Rothman, and José R. Solórzano. 2011a. Improving Global Health. Vol. 3 of the Patterns of Potential Human Progress series. Boulder, CO, and New Delhi, India: Paradigm Publishers and Oxford University Press.
Hughes, Barry B., Randall Kuhn, Cecilia M. Peterson, Dale S. Rothman, José R. Solórzano, Colin D. Mathers, and Janet R. Dickson. 2011b. "Projections of Global Health Outcomes from 2005 to 2060 Using the International Futures Integrated Forecasting Tool." Bulletin of the World Health Organization 89(7): 478–486. DOI: 10.2471/BLT.10.083766.
Milante, Gary, Barry B. Hughes, and Alison Burt. 2016. “Poverty Eradication in Fragile Places: Prospects for Harvesting the Highest Hanging Fruit by 2030.” Stability: International Journal of Security and Development 5(1): 1–24. DOI: 10.5334/sta.435.
Moyer, Jonathan D., and Barry B. Hughes. 2012. "ICTs: Do They Contribute to Increased Carbon Emissions?" Technological Forecasting and Social Change 79(5): 919–931. DOI: 10.1016/j.techfore.2011.12.005.
Rothman, Dale S., Mohammod T. Irfan, Eli Margolese-Malin, Barry B. Hughes, and Jonathan D. Moyer. 2014. Building Global Infrastructure. Vol. 4 of the Patterns of Potential Human Progress series. Boulder, CO, and New Delhi, India: Paradigm Publishers and Oxford University Press.
Note: Energy trade is represented in a 'pooled' approach - imports and exports are aggregated across energy types.